问题描述

Qsymmetry是基于Python应用群论分析物理系统的对称性求解系统Hamiltonian的计算包，它可以一定程度上简化我们对物理系统对称性的分析过程，但是官方教程缺少直观的图像说明，函数参数信息不详，本文意在详细说明Qsymm函数和对应参数的物理含义，降低其学习的难度。

群论和对称性

对称性研究在整个物理学领域占据了重要的位置，描述对称性的数学工具是群论，而物理系统通常涉及的是对称变换，包括系统的平移、旋转以自身在度量空间的对称性，系统所有对称性变换的集合构成对称变换群。

群的线性表示

量子态是在希尔伯特空间中描述，对称性变换不改变系统的物理性质，只能是幺正或者反幺正变换，幺正条件保证了线性变换矩阵的正交性，而反幺正变换主要用于描述分立对称性中的时间反演对称性，对应变换是反线性的。

构成群的条件

对称性变换满足成群的条件：

存在唯一幺元

$$D(E)=\boldsymbol {1}.$$

每一群元素对应存在唯一逆元

$$\quad D(R)D(R)^{-1}=\boldsymbol {1}.$$

封闭性

$$D(R_1)D(R_2)=D(R_3).$$

群乘法满足结合律

$$[D(R_1)D(R_2)]D(R_3)=D(R_1)[D(R_2)D(R_3)].$$

群的正则表示

群只有乘法，但是可以通过群元作为基矢量张成的群空间构造群代数，定义矢量的加减法、系数乘法以及矢量与矢量间的乘法，并满足对应封闭性，并满足分配律，即可得到群代数。（群代数对于深化群的认识和应用有重要意义，这里只做引入）

定义群代数的矢量

$$X=\sum_{R\in G}f(R)R.$$

很容易证明有限群任意矢量满足群代数的要求。

任何有限群都有一个真实线性表示，称为正则表示，利用群代数可以给出有限群的正则表示。因为在群代数中群元素既是矢量也是算符，作为算符满足群的乘积规则。

$$SR=T=\sum_{P\in G}P D_{PR}(S),\\ D_{PR}=\left\{\begin{matrix}1,&P=SR\\0,&P\neq SR\end{matrix}\right..$$

一旦给出群的乘法表，便很容易得到群的正则表示$D(G)$。

以二面体群$D_3$为例，其乘法表

$$\begin{array}{c|cccccc} \hline D_3& E & D & F & A & B & C \\ \hline E & E & D & F & A & B & C \\ D & D & F & E & B & C & A \\ F & F & E & D & C & A & B \\ A & A & C & B & E & F & D \\ B & B & A & C & D & E & F \\ C & C & B & A & F & D & E \\ \hline \end{array}$$

可以给出

$$D(E)=\mathrm{dignal}(1,1,1,1,1,1),\\ D(D)=\left(\begin{array}{llllll} 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right),\\ D(A)=\left(\begin{array}{llllll} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right),\\ \cdots.$$

群的一般性质

群具有以下特征

子群和重要的集合

子群：

群元素的个数即群的阶。只要按照群乘法规则满足成群条件，群G的子集H也可以构成群，即群G的子群。任何群都有幺元和自身这两个平庸的子群。

陪集：

由于群乘法的特点，我们可以由群的子群H

$$H=\{S_1,S_2,S_3,\cdots,S_h\}\quad S_1=E$$

分别定义子群的左陪集和右陪集

$$\begin{matrix}R_jH=\{R_j,R_jS_2,R_jS_3,\cdots,R_jS_h\},\\ HR_j=\{R_j,S_2R_j,S_3R_j,\cdots,S_hR_J\}.\end{matrix}\qquad R_j\in G\quad R_j\notin H.$$

其中h是子群的阶。之所以定义陪集，一个重要的原因在于可以利用陪集完成对群的划分。

$$G=H\cup R_2H\cup R_3H\cup\cdots\cup R_dH,\quad g=dh.$$

由此可见，群G的阶如果是素数，该群一定不存在非平庸的子群。相反，如果群G的阶可以分解因子$g=mn$，一定可以得到G的子群的阶为$m$或$n$。如果子群H的左陪集等于右陪集，那么该子群就是不变子群或叫正规子群。由不变子群可以定义群G的商群：

$$Q=G/H.$$

可以看出，不变子群H就是商群的幺元，也只有不变子群可以满足群G存在商群的条件。

共轭类：

共轭类在物理学中的群论有重要应用，幺正变换沟通了不同表象下的物理量，而对称性变换一般就是幺正变换，而共轭类$\mathcal C_\alpha$描述的就是由群元$S$沟通具有某种共同性质群操作：

$$R'\longleftrightarrow SRS^{-1}.$$

记作：

$$\mathcal C_\alpha=\{R_1,R_2,\cdots,R_{n(\alpha)}\}=\{R_k|R_k=SR_jS^{-1},\,S\in G\},$$

$n(\alpha)$是类元素的个数。

容易看出，如果取定群元$S$，$R_j$取遍类中所有元素，对应共轭元素不会有重复，而取定类元素$R_j$,$S$取遍群G的元素，类中共轭元素$R_k$一定会重复出现$m$次，使得$n(\alpha)=g/m$。这保证了两个类不会有重复元素。共轭类这个特点从物理图像上相当于描述同一类对称性变换，比如一个空间群中二次轴旋转和四次轴旋转是分属不同的类，通俗地讲，该空间群可以有二次轴类和四次轴类。

由此我们可以根据共轭类的属性将群G按照类的不同进行划分

$$G=\{E,\mathcal C^1_{n(\alpha)},\mathcal C^2_{m(\alpha)},\cdots,\mathcal C^l_{n'(\alpha)}\}.$$

定义的群元的阶$n$

$$\underbrace{R\times R\times\cdots\times R}_n=R^n=E$$

共轭类的性质决定了同一个共轭类中所有类元素具有相同的阶，因为

$$[(D(S)D(R)D(S)^{-1}]^n=D(S)D(R)^nD(S)^{-1}=D(E).$$

这个特点决定了我们找共轭类只需要在阶数相同的元素中判断。

群的生成元：

由群元素阶的定义，可以看出一个完整的循环群$C_n$可以由一个群元素$R$的有限幂次来表达，$R$称为该循环群的生成元，$n$是循环群的阶。这是有限群中去群生成元的定义，往往一个有限群具有一个以上的生成元，比如二面体群$D_3$就有翻转操作和旋转操作两个群生成元，它们的阶数分别是2和3。

容易混淆的是，对于连续群，比如在物理研究中应用最广泛的李群，定义连续群的生成元为

$$T_{a} \equiv-\left.i \frac{\partial \mathcal{R}\left(e^{a}, \omega\right)}{\partial \omega}\right|_{\omega=0}.$$

对于三维转动群$R( \hat{ \boldsymbol {n}},\omega)=\exp(-i\omega T\cdot \hat{\boldsymbol {n}})$，则三维转动的生成元为

$$T_{1}=\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -\mathrm{i} \\ 0 & \mathrm{i} & 0 \end{array}\right),\\ T_{2}=\left(\begin{array}{ccc} 0 & 0 & \mathrm{i} \\ 0 & 0 & 0 \\ -\mathrm{i} & 0 & 0 \end{array}\right),\\ T_{3}=\left(\begin{array}{ccc} 0 & -\mathrm{i} & 0 \\ \mathrm{i} & 0 & 0 \\ 0 & 0 & 0 \end{array}\right).$$

同Pauli矩阵非常相似，的确，二维幺正幺模群SU(2)正是三维转动群SO(3)的覆盖群。而连续群的生成元则是微分算符在表示空间的矩阵形式，如此就可以带入量子力学的概念，引入厄密算符和幺正算符的对应。

自逆类和相逆类

一个类中的元素$R_j$的逆元也构成对应的类，所谓“逆类”

$$R_{i}=S R_{j} S^{-1}, \quad R_{i}^{-1}=S R_{j}^{-1} S^{-1}\\ \mathcal C_\alpha\rightarrow \mathcal C_\alpha^{-1}$$

$\mathcal C_\alpha$和$\mathcal C_\alpha^{-1}$成为相逆类，如果二者重合则称为自逆类。

从置换群看共轭类：

置换群可以写成一系列轮换乘积的形式，对应置换的一个轮换结构。

一个置换可以写作：

$$R_1=\begin{pmatrix}1&2&3&4\\2&3&4&1\end{pmatrix}=\begin{pmatrix}4&2&1&3\\1&3&2&4\end{pmatrix}=(1,2,3,4),\\ R_2=\begin{pmatrix}1&2&3&4\\4&2&1&3\end{pmatrix}=\begin{pmatrix}3&2&4&1\\1&2&3&4\end{pmatrix}=(1,3,4)(2)=(1,3,4).\\$$

两个置换乘积：

$$\begin{aligned} R_1 R_2&=\begin{pmatrix}1&2&3&4\\2&3&4&1\end{pmatrix}\begin{pmatrix}3&2&4&1\\1&2&3&4\end{pmatrix}=\begin{pmatrix}3&2&4&1\\2&3&4&1\end{pmatrix}\\&=\begin{pmatrix}4&2&1&3\\1&3&2&4\end{pmatrix}\begin{pmatrix}1&2&3&4\\4&2&1&3\end{pmatrix}=\begin{pmatrix}1&2&3&4\\1&3&2&4\end{pmatrix}=(2,3)(1)(4)=(2,3) \end{aligned}$$

置换群$\mathcal S_3$写成轮换的形式：$\mathcal S_3=\{I,[2\,3],[1\,3],[1\,2],[1\,2\,3],[3\,2\,1]\}$

置换群$\mathcal S_4$写成轮换的形式：

$$\mathcal S_4=\{I,[1,2,3,4],[4,3,2,1],\cdots\}$$

置换群$\mathcal S_n$的类由$n$的配分数描写，$n$的配分数即不同轮换结构的数目。$n$个序列的一个置换对应一个轮换结构，构成一种配分数：

$$\sum_i\mathcal l_i=n.$$

晶体空间群对称素和共轭类：

空间群的对称素有三种

• n次旋转对称轴，其中n=1,2,3,4,6
• 对称心，即空间反演对称，记为$i$
• n次旋转反演对称轴，顾名思义，是对体系某旋转对称轴先作用n次旋转操作，然后作用空间反演，整个过程满足对称条件。记为$\overline n$。

值得注意的是，这三种对称素构成了一些晶体空间群中非常直观的概念，比如旋转反演$\overline 2$实际上是一个镜像操作，$\overline 6$是一个三次轴加镜像的操作。

晶体空间群对称素的概念实际上和群的共轭类有直接的联系。这里以$D_{6h}$群直观说明：

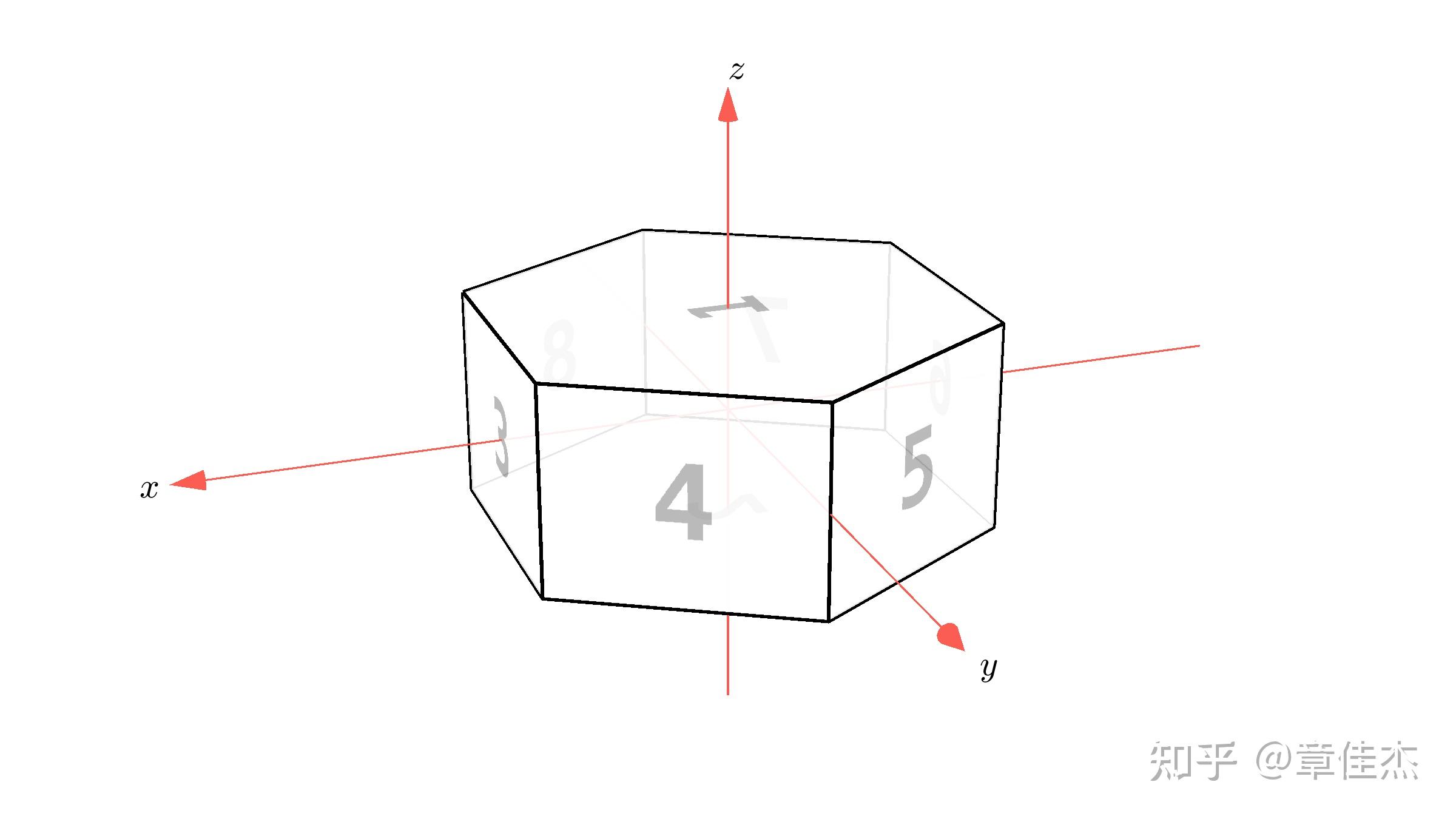
对于这样一个棱柱，显然就有一个六次轴，6个不同的二次轴。$D_{6h}$有24个群元，它是$D_6$群作用一个水平反演的结果，用群论的语言即$D_{6h}=D_{6}\otimes V_2$，由两个子群直积而来。而$D_6$群有12个群元，分别包括6阶循环群或6次旋转群$C_6$的六个群元

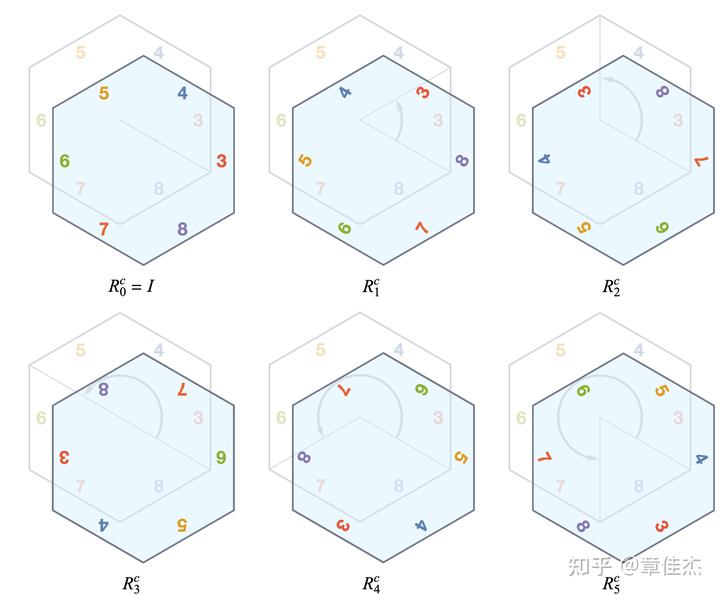
以及二次轴翻转构成的六个群元

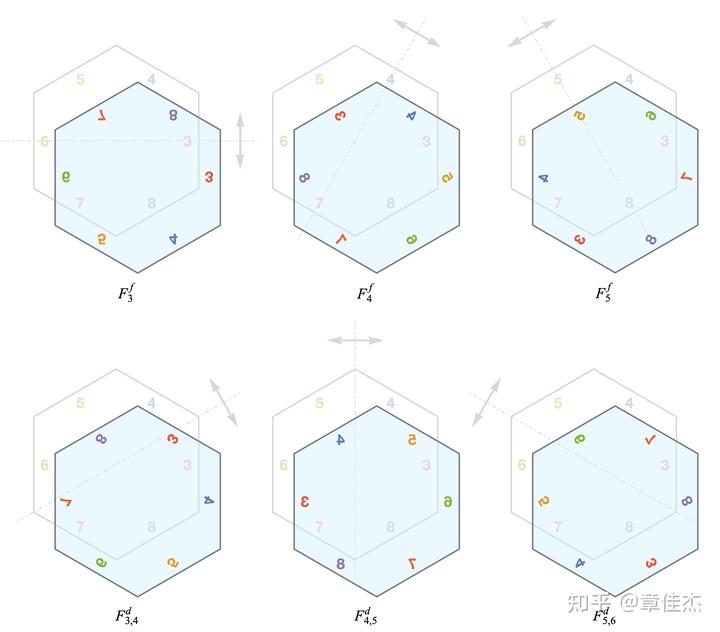
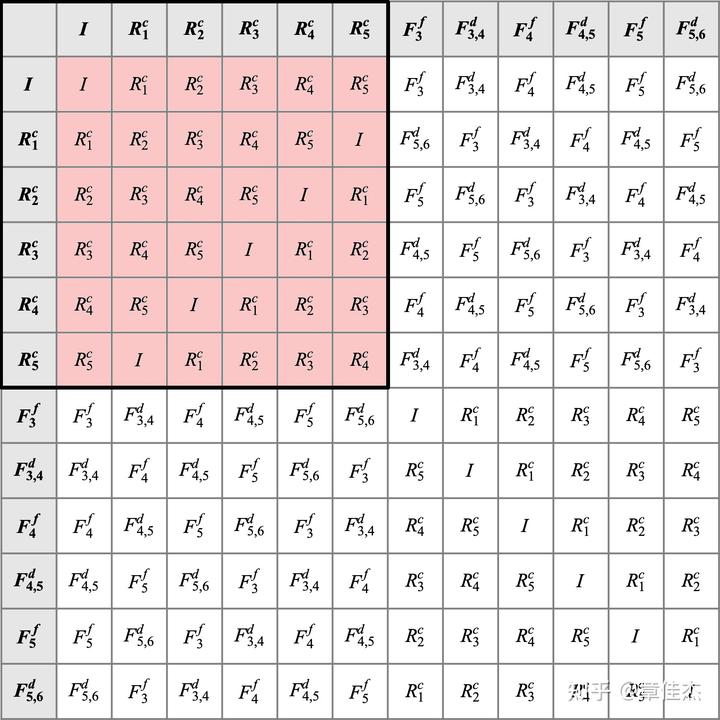
共同组成。其中六次转动把两次转动联系起来，幺元构成一类，六次轴构成一类，两个二次轴各自构成一类，所以$D_{6h}$具有四个类，四个类都是自逆类。这里面判断可以由乘法表给出，因为

$$(ST)=S(TS)S^{-1}.$$

所以我们只需关注乘法表对角线的元素。

同构和同态

这两个概念联系了群论中一个应用很广泛的概念：映射。定义映射$\psi:G\rightarrow H$。首先$\psi$是保群映射，满足

$$\psi(D(R))\psi(D(R'))=\psi(D(R)D(R'))\\ \psi(D(R)^{-1})=\psi(D(R))^{-1},\quad \psi(D(E))=h_e$$

根据这个条件可以给出对原群的逆元和幺元的一一映射，保证了群的生成。因此如果映射是单射且满射，则在该映射下原群和新群同构，如果仅仅只是单射，则两群同态。

幺正表示和特征标表

有限群的线性表示是以舒尔定理为保证的，这里只贴出重要的结论不多做介绍和证明，详见各种群论教材。

对称群幺正表示的约化

$$G(R) \Rightarrow D(R) \Rightarrow X^{-1} D(R) X=\oplus_{i} a_{i} D^{i}(R)$$

有限群不等价不可约幺正表示的正交性：

$$\sum_{R \in G} D_{\mu \rho}^{i}(R)^{*} D_{\nu \lambda}^{j}(R)=\frac{g}{m_{j}} \delta_{i j} \delta_{\mu \nu} \delta_{\rho \lambda}$$

随即可以得到特征标正交：

$$\sum_{R \in G} \chi^{i}(R)^{*} \chi^{j}(R)=g \delta_{i j} .$$

一个重要的推论：

$$\sum_{R\in G}|\chi(R)|^2=g.$$

它是有限群不可约表示的充要条件。
但是从物理的角度出发，一个可测的物理系统涉及的对称变换包括各种表象变换毫无疑问都是幺正变换，这是量子力学基础的内容。所以群的线性表示论的核心就是以线性空间来描述群空间，寻找群的不等价不可约表示。这样的概念可以直接过渡到复数域，利用共轭类的特性给出有限群的特征标。比如二面体群有三个类，三个类都是自逆类，所以特征标都是实数。

$$\begin{array}{c|ccc} \hline D_{3} & E & 2 C_{3} & 3 C_{2}^{\prime} \\ \hline A & 1 & 1 & 1 \\ B & 1 & 1 & -1 \\ E & 2 & -1 & 0 \\ \hline \end{array}$$ $$\begin{array}{c|cccccc} \hline C_6 & E & R & R^{2} & R^{3} & R^{4} & R^{5} \\ \hline A & 1 & 1 & 1 & 1 & 1 & 1 \\ B & 1 & -1 & 1 & -1 & 1 & -1 \\ E_{1} & 1 & -\omega^{*} & \omega & -1 & \omega^{*} & -\omega \\ E_{1}^{\prime} & 1 & -\omega & \omega^{*} & -1 & \omega & -\omega^{*} \\ E_{2} & 1 & \omega & \omega^{*} & 1 & \omega & \omega^{*} \\ E_{2}^{\prime} & 1 & \omega^{*} & \omega & 1 & \omega^{*} & \omega \\ \hline \end{array}\\ \omega=\exp \{-\mathrm{i} 2 \pi / 3\}$$ $$\begin{array}{c|cccccc} \hline \mathrm{D}_{6} & E & 2 C_{6} & 2 C_{6}^{2} & C_{6}^{3} & 3 C_{2}^{\prime} & 3 C_{2}^{\prime \prime} \\ \hline A_{1} & 1 & 1 & 1 & 1 & 1 & 1 \\ A_{2} & 1 & 1 & 1 & 1 & -1 & -1 \\ B_{1} & 1 & -1 & 1 & -1 & 1 & -1 \\ B_{2} & 1 & -1 & 1 & -1 & -1 & 1 \\ E_{1} & 2 & 1 & -1 & -2 & 0 & 0 \\ E_{2} & 2 & -1 & -1 & 2 & 0 & 0 \\ \hline \end{array}$$

SO(3)和SU(2)

SO(3)即三维特殊正交群，三维旋转群是SO(3)。旋转操作的算符形式为

$$e^{-i\frac{\boldsymbol {J}\cdot\boldsymbol {n}\phi}{\hbar}}.$$

所以三维旋转变换总是可以写成正交矩阵的形式。樱井在《Modern Quantum Mechanics》角动量一章详细介绍三维转动系统和二分量旋子系统。他利用无穷小转动的技术结合前一章平移变换的讨论阐述了转动算符的由来。

首先，这里面的$\boldsymbol {J}$是旋转操作的生成元，因为旋转算符在无穷小转动下是$1-iJ\Delta \phi/\hbar$。

根据欧拉转动

$$\mathcal{D}(\alpha, \beta, \gamma)=\mathcal{D}_{z}(\alpha) \mathcal{D}_{y}(\beta) \mathcal{D}_{z}(\gamma).$$

我们可以引入一个特殊的转动或者正交变换$S(\psi,\theta)$

$$S(\varphi, \theta)=R\left(\vec{e}_{3}, \varphi\right) R\left(\vec{e}_{2}, \theta\right)=\left(\begin{array}{ccc} \cos \varphi \cos \theta & -\sin \varphi & \cos \varphi \sin \theta \\ \sin \varphi \cos \theta & \cos \varphi & \sin \varphi \sin \theta \\ -\sin \theta & 0 & \cos \theta \end{array}\right).$$

显而易见，这个操作是可以把$z$轴上的点转到$\hat{\boldsymbol {n}}(\psi,\theta)$方向，$\theta$和$\psi$确定了球坐标的极角和方位角。所以

$$ST_3S^{-1}=\hat{\boldsymbol {n}}T.$$

进而可以给出一个重要关系

$$\begin{aligned} R(\hat{\boldsymbol n}, \omega) &=S(\varphi, \theta) R\left(\vec{e}_{3}, \omega\right) S(\varphi, \theta)^{-1}=\exp \left\{-\mathrm{i} \omega S T_{3} S^{-1}\right\} \\ &=\exp \{-\mathrm{i} \omega \hat{\boldsymbol n} \cdot \vec{T}\}=\exp \left\{-\mathrm{i} \sum_{a=1}^{3} \omega_{a} T_{a}\right\} \end{aligned}.$$

可见任何可能的转动$R(\hat{\boldsymbol n}, \omega)$都与相应的$R\left(\vec{e}_{3}, \omega\right) $共轭, 或者说同类，他们之间差一个正交变换。关系式直接给出了维格纳公式。于是我们可以看出

$$R(\hat{\boldsymbol n}, \omega)=R(-\hat{\boldsymbol n}, 2 \pi-\omega), \quad R(\hat{\boldsymbol n}, \pi)=R(-\hat{\boldsymbol n}, \pi).$$

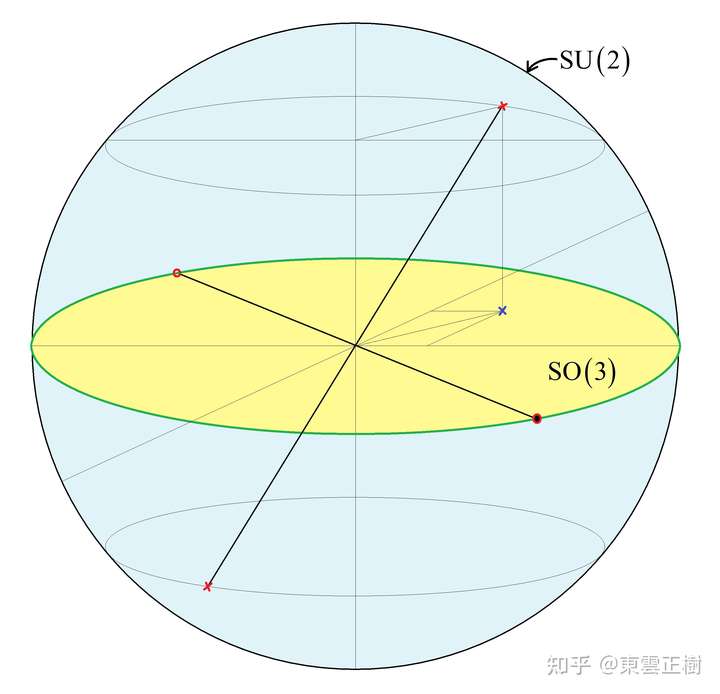
所以三维转动是在半径为$\pi$的球内连续变化，在球面上直径两端的点代表同一转动。

类似地，可以给出二维幺正幺模群SU(2):

$$\exp \left(\frac{-i \sigma \cdot \hat{\mathbf{n}} \phi}{2}\right)=\left|\begin{array}{ll} \cos \left(\frac{\phi}{2}\right)-i n_{z} \sin \left(\frac{\phi}{2}\right) & \left(-i n_{x}-n_{y}\right) \sin \left(\frac{\phi}{2}\right) \\ \left(-i n_{x}+n_{y}\right) \sin \left(\frac{\phi}{2}\right) & \cos \left(\frac{\phi}{2}\right)+i n_{z} \sin \left(\frac{\phi}{2}\right) \end{array}\right|.$$

注意到幺正幺模的条件，对SU(n)

$$SU(n):\{U|U\in \mathrm GL(n,\mathbb C),U^\dagger U=\boldsymbol {I},|U|=1\}.$$

具体到SU(2)

$$SU(2):\left\{\left[\begin{array}{cc} a & b \\ -b^{*} & a^{*} \end{array}\right]|a, b \in \mathbb{C},| a|^{2}+|b|^{2}=1\right\}.$$

SU(2)和SO(3)（图源:见水印）

Qsymm主要的模块

Qysmm是一个python程序包，其中包含了一系列对称性模块和算法：

import qsymm

给出模型的对称性分类

我们可以利用Qsymm中的对称性分类模块寻找已有模型的所有对称性。当然

H = qsymm.Model(ham)#利用model模块可以给出对应矩阵的展开形式
cubic_group = qsymm.groups.cubic()#Qsymm预置的群类，这里是立方体O群
discrete_symm, continuous_symm = qsymm.symmetries(H, cubic_group)#利用symmetries模块，依据主要参数可以给出系统所有存在的对称性，包括离散对称性和连续对称性。这里cubic_group的arg是候选晶体点群，迭代算法找到系统与之匹配的对称性。
print(len(discrete_symm), len(continuous_symm))
qsymm.PointGroupElement(R=np.diag([1, -1]), U='kron(sigma_y, sigma_z)')#利用点群模块PointGroupElement可以直观显示对应幺正表示的对称性操作。示例给出的是二维系统关于x轴的镜像。

导出连续性模型

利用对称性变换关系

$$\begin{aligned} P_{R} \psi_{\alpha}(\boldsymbol k) &=\sum_{\beta} \psi_{\beta}(\boldsymbol k) D_{\beta \alpha}(R) \\ H(\boldsymbol k) &=P_{R} H(\boldsymbol k) P_{R}^{-1} \end{aligned}$$

可以通过已知对称性操作导出连续性模型的Hamiltonian，所以预先需要确定所要研究的系统全部对称性。

利用Qsymm对称操作模块，这里简要给出一些示例：

TR = qsymm.time_reversal(实空间维度， 幺正矩阵U，spin（整数或半整数或给出三个对应角动量矩阵）) #这里是离散对称性中的时间反演对称性。可选择地利用对称性操作的幺正表示或者系统的自旋角动量确定该对称性，下同
Mx = qsymm.mirror(镜像轴[1, 0]，幺正表示U，spin （整数或半整数或给出三个对应角动量矩阵）) #这是镜像对称性
IN = qsymm.inversion(实空间维度,幺正矩阵U) #这是空间反演对称性
C = qsymm.chiral(实空间维度,幺正表示U) #这是手征对称性
Cn = qsymm.rotation(1/n, 旋转轴，反演操作(默认false, 幺正矩阵U), 角动量)#这是点群中最为基础的旋转对称性。这里n={1,2,3,4,6}为晶轴旋转，U的维度决定不可约表示的维度

利用这些已有的对称性，通过对称变换约束性关系，可以利用continuum_hamiltonian模块直接给出我们需要的连续性模型。

dim = 2           #模型维度
total_power = 3      #动量的阶数
family = qsymm.continuum_hamiltonian(symmetries, dim,total_power, prettify=True) #这里symmetries即我们预先确定的系统的对称性，dim是系统的维度，total_power是动量的阶数。

导出紧束缚模型

紧束缚模型的导出和连续性模型类似，需要预先确定体系的对称性，给出对称性的过程和连续性模型的一致。

唯一不同的是利用Qsymm的Bloch_family模块导出紧束缚模型还需要确定最近邻原子轨道间的hopping，通常需要给体系不同原子做标记，并给出对应原子的轨道数，然后利用hopping vector最终确定最近邻hopping的紧束缚模型。

norbs = [('a', 3)] #标记为a的原子有三个轨道，体系只有一种原子。
norbs = [('A', 1), ('B', 1)] #标记为A和B的原子各自有一个轨道，体系有两种原子。
hopping_vectors = [('a', 'a', [1, 0])] #定义a原子和a原子的最近邻hopping，hopping矢量是默认的[1,0]
hopping_vectors = [('A', 'B', [0, 1])]#定义A原子和B原子的最近邻hopping，hopping矢量是[0,1],表示从B的轨道hopping到A的轨道。
family = qsymm.bloch_family(hopping_vectors, symmetries, norbs)#bloch_family模块三个主要参数即可确定体系的紧束缚模型，分别是hopping矢量，对称性集合，以及对于原子标记及轨道数。
qsymm.display_family(family